Once upon a time we had a dream. It involved a couple hundred of you, 35 of us, a group retreat site in the San Bernadino Mountains and a weekend packed with workshops, panels, activities and performances designed to inspire, educate, entertain and/or make you laugh — basically, it was the spirit of this website manifested in three entire dimensions. We wanted to create a special (and affordable!) space where you could be yourself, enhance your relationships within the international queer community, support Autostraddle and make new friends forever.
It was a dream called A-Camp, and it was a dream that came true the last weekend of April, 2012.
So we’re doing it again.

Details
+
When:
Wednesday September 12th – Sunday September 16th
+
Where:
Alpine Meadows Retreat Center in Angelus Oaks, California. It’s 1.5 hours from Palm Springs, 2 hours from Los Angeles, 2.5 hours from San Diego, 4 hours from Las Vegas, 5 hours from Phoenix and 8 hours from San Francisco. We’ll be running shuttles from LAX to the campsite from 10 AM to 3PM on September 12th and shuttles back to LAX from 9AM until 3PM on September 16th.
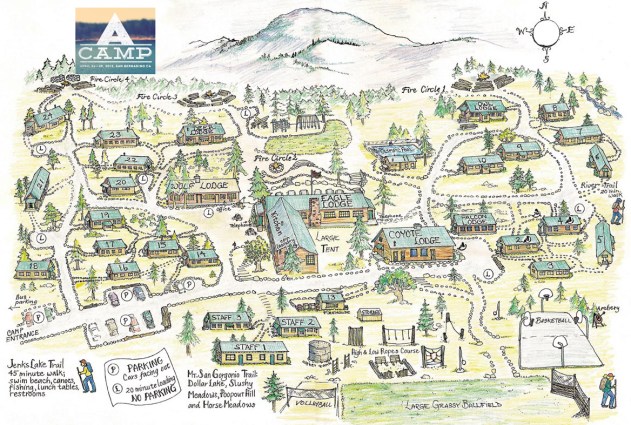
+
Lodging:
You’ll be having the bestest biggest surprise slumber party of your life in fully insulated, carpeted & heated cabins with private bathroom/showers/baths and generously-sized bunk beds. You’ll be sharing these cabins with somewhere between 5 and 17 other female-identified humans. Cabin groups are designed with your needs in mind (we meet all roommate requests!) and are headed by Counsellors from Team Autostraddle.

+
Who:
You weirdos! Anyone over the age of 18 is welcome — in April, our campers ranged in age from 18 to 49 and came from all over the world. This time, we’ve got exclusive use of the site all week and will be doubling enrollment.
+
How:
Tuition is $365.
Just $50 down reserves your spot!
+
Your tuition includes:
+ Four nights lodging
+ Three meals a day and snacks (with vegan, vegetarian, gluten-free and kosher options)
+ Full access to a variety of daytime programming situations, ranging from arts+crafts to morning hikes to panels/workshops.
+ Special Guests: The entire event will be MC’ed by world’s funniest duo, Julie Goldman and Brandy Howard and you’ll be seeing a lot of the beautiful ladies of Unicorn Plan-It.
+ Kickass gift tote packed with amazing things such as an A-Camp T-shirt you can sell on ebay in ~4 years

+
What the hell goes on at A-Camp?

+
For more information about what goes on at A-Camp, you can check out our recaps from April’s camp and testimonies from campers about the joy of the experience. Keep in mind that this time around, things will be even more awesome.
Days at A-Camp are spent participating in a variety of programming options offered by the Autostraddle Team and special guests — Speed-Dating with Hannah Hart! Gender Panel! Poetryfest! Lesbian Jeopardy! Style Workshop! Sewing Circle! How to Pick Up Chicks! Writing Workshop! Picking Up Chicks! High Tea! ‘Zine-making! We’ll have a whole slate of brand-new and/or improved activities in September, including panels/workshops on topics like “Trans* 101,” body image and queer religion/spirituality.

+
Every night offers plenty of opportunities for fun-fun-fun, including the All-Camp Talent Show (hosted by Julie & Brandy), DJ Carlytron’s T-Dance, Julie & Brandy’s Trivia Extravaganza and campfires to gather ’round and sing Indigo Girls and/or eat S’Mores.

Okay, I’m in. What Now?
If you wanna get on the saddle and trot on over to A-Camp with us this fall, here’s what you’ve gotta do:
1. For the low low price of a $50 non-refundable deposit (and $3.21 “service charge” from the registration interface — you’ll only have to pay this once), you can snag your spot for the fall festivities. Answer a couple questions about yourself and you’re good to go.
2. When registration fills up, you can put yourself on the waitlist. Be sure to put an e-mail address you check regularly & often, so you don’t miss our note if you’re up!
3. On or before June 5th, we’ll update the registration interface to include options for paying your tuition, questions about your travel plans, rooming/bunking needs, dietary desires and other special feelings.
4. If you’re driving in on Wednesday, please plan to arrive between 12:00 noon and 5:30 PM. On Sunday, please plan to leave around 1 PM.
5. If you’re looking for flights and will need transportation from the airport, then please book your incoming flights for Wednesday, September 12th to get in by 3 PM at the latest. Camp officially begins at 6 PM. There will be activities going on throughout the afternoon, but mostly we want to allow you time to get settled in before your counsellors take you into the woods and brand you for life while howling at the moon.
If you’ll need transportation to the airport on Sunday, September 16th, then please try to get a flight that leaves after 1pm. There will probably be stuff happening on Sunday morning, and if you wanna be there for that stuff, try to get a flight after 6PM.
If those travel specifications are totally absolutely impossible for you, email a.camp.september at gmail dot com to make special arrangements.
6. If you need to cancel, you can just log back in to the registration interface and cancel!
Quick Note on Workshops
If you’ve secured your spot at camp and are a specialist in your field or have a super-special skill you think would make a great addition to the schedule, then we are accepting workshop proposals from campers. Please get yours in to Marni & Robin by July 1st. These workshops/panels/activities should be unique ideas specific to your background and skill-set (aka, things we couldn’t do ourselves without you) — in April, we had a camper teach Crossfit and another lead a workshop in Circus Acrobatics For Everyone.
If you’re interested in participating in an Autostraddle-populated panel, we’ll have more information on that later this summer when we finalize the list of panels that we’re doing. In April, we had two campers join Katrina and Carmen in leading the Activism Workshop and another camper with a relevant background appeared on our fantastic Sex Panel.
We do not accept applications for Camp Staff or counselor positions, those are all handled in- house.
FAQ:

Q: How do you win camp?
Q: I’m really super poor but I want to go so bad!
A: Firstly, this is a once-in-a-lifetime Utopia-esque situation, I recommend getting your emergency funds out. But we get that hard times are here for some of you, and that’s why we’ll offer two ways to pay — upfront in June or in installments throughout the summer. No fees, no gimmicks, no credit checks. We’ll work with you to get you there. That’s just how much we want you to come.
You can also apply for a “Campership.”
Q: Is there Wi-Fi?
A: NOPE! I know it’s scary!
Q: Will there be any free time?
A: Yup! I mean you don’t have to do anything you don’t want to do. Go read by the river or go videotape your friend hiding in a tree like a monkey or just lie on the grass or in your bed. You can do whatever you wanna do, you’re a grown-up!
Q: What’s the deal with alcohol?
A: Drinking isn’t part of any A-Camp activities and we do not serve alcohol. But if you’re over 21 and wish to drink at camp, you have to bring your own alcohol, put your name on it, and store it in one of our designated lodges (food/drink are prohibited in cabins because of bears) where you can access it whenever you want. We’ll be providing a “sober cabin” option for anyone over 21 who would prefer to room with other abstainers.
Q: Are there extra charges for any activities?
A: Yes. We’re not positive about the shuttle cost yet, but I think it’s gonna be a $25 fee each way for those requiring transportation to/from LAX. There’s also a $20 fee for the Ropes Course or Climbing Tower, and a $10 fee for linens. You’ll get the chance to put money down for those things later.
Q: Me and my girlfriend/all my friends want to go together, can we stay in the same cabin?
A: Yes.
Q: I can’t come to camp but would like to help somebody else get there, can I do that?
A: Absolutely! Just go right here.
Q: When are you doing an East Coast camp?
A: I know this seems like SUCH a good idea! But for a zillion reasons including a shorter off-season and the fact that most of our team lives on the West Coast, this simply isn’t affordable or logistically possible for us right now — and in turn, for you. This is something we hope to do in the future but we’re not sure when that will be yet, so don’t hold your breath. However, it’s worth noting that we picked a site near LA because it’s one of the cheapest airports to fly into in the country. Have you been to California in the fall? It’s really nice, it’s basically summertime.
Q: What about A-Camp in CANADA?!
A: The expenses required to put on A-Camp in any other country would drive your cost to about $2,000 for a weekend, and that’s before plane tickets, passport fees, etc. If we ever do an international A-Camp, it would be years from now.
Q: When is the next camp after this camp?
A: We’re not 100% positive yet, but it will probably be in May at the same site.
Q: What’s that link again?
A: Here it is!
Q: Anything else?
A: Please we beggeth of you from the deepest depths of your beating heart, to make sure we have an email address for you that you check often. We will be sending you updates via e-mail and it’s imperative that you receive and respond!
Also! Marni & Robin are the contacts for A-Camp questions as they are A-Camp directors. You can reach them at a.camp.september at gmail dot com and robin at autostraddle dot com.



Okay 1000 of your page views today were me, but it was totally worth it. I might pass out with joy.
u 2 eh? i know i was checking so much cause i had a final this morning and didnt want to miss it!
(also im liking your post. dont know how to make it a +5)
You have to register first.
so many opportunities to register for things today!
Hey if you do it in May next year I can justify it as a birthday present again! Well actually I probably won’t be going unless I win the lottery.
21st birthday: September 9. 21st birthday present: September 12-16. Hot damn.
hey my birthday is one day before yours :)
and mine is one day after! Group birthday celebration at camp?!
Posts about camp sort of make me sad, because there is no way in hell I’ll ever be able to afford $365 plus a plane ticket to California. And seeing y’all being excited about it makes me feel left out :(
Keep your eyes open for a post about A-Camp scholarships this week!
I just registered, but if by some chance come September a.) I have a job and b.) the Chicago teachers union isn’t on strike, I hereby bequeath my spot to you. If neither of those things happen, I’ll help sponsor you. Fret not, fellow queer, we have your back!
And now I just remembered that I have a wedding in Michigan that weekend…fuck.
Seems like a good time to say, “I’m not going to any weddings until I can get married, too”, right?
campership post!
http://www.autostraddle.com/a-camp-september-2012-its-campership-time-138216/
I wish.. If only I hadn’t used up all my vacation days already. Maybe next year…
Wooh! I registered.
There was a 49 year old old at A Camp?! How do I not know this person? I thought I was the resident elder around here. #autostraddledenmother
I knew there were a few as/older than me but I didn’t know they went to camp!
Bring on A-Camp 2.0!
Nah. Didn’t go to camp, but I hang out here a lot
And I’m 60.
I’ve been refreshing the page for the past 3 hours. This is gonna be my graduation/birthday present, if I can scrape up the down payment in time. So. Damn. Excited.
Registered. Duh.
Yay! Also we need to hang soon.
Remember me from Friday night, Sondra?! Anyhoo, I just registered too… We soooo need to hang out soon.
HECK YEAH.
My credit cards will hate me. DON’T CARE. This time.
We’ll be poor, together, Marika. Just like always.
Haters gonna hate
To hell with mastercard
Listling Without Commentary: Marika’s Allergies
It should be Marika’s allergic reactions. That would be even funnier.
severe ear pain
tummyaches
weird rash on hand
swollen tongue
etc
Beth is going to have an extra fun time this session!
The US has never felt so far away goddamnit
sniff sniff. if only! uk dwellers like myself can only dream longingly of california sunshine and american lesbos
We should totally organise a British/European A-Camp for all of us who are unable to make the trip over the Atlantic!
that’s a brilliant idea. it would be so much fun! how could we organise something like that?
maybe we should start a group or page where we could organise it together?
I have no relevant organisational skills but I would absolutely come to this if it happened.
I just went on the groups page to try and make one for organising this but it refuses to load. D: But I’m totally up for helping organise a camp/meet-up here in europe! :) I think we would need more input to actually make any decisions?
I would be there unbelievably!
I would cross the hell of that Channel if you make UK Camp happen.
Uk camp!
I might have to eat ramen and peanut butter for a year, but dammit, I will find a way. *registered* That said, I won’t know my school schedule until August, and nursing school isn’t kind about missing an exam unless you’re in the process of some life-threatening thing…do you know the last day that you can cancel for most of your money back?
Happy dance/flailing like an idiot time. AHHH!
the last day you can cancel and get any percentage of your money back would be August 12th — if you want a full refund (everything but the deposit), then you’ll need to cancel before August 1st. We’ll lay out all these dates for you when we get into the money stuff.
but more importantly YAY CAMP!!!!
So not only did I JUST find out I can’t finish paying for acamp but I also just read this. I believe this is the part where I start having a nervous breakdown while planning how I will begin tricking myself out to finish paying for this so as to not let the money I’ve already put into it go to waste.
Registered! I AM SO EXCITANT.
Hahaah that made me laugh out loud here
oh my.
this feels surreal. and really expensive.
Amen to that. but I always get really excited when the amount is being converted into €uro and gets a tiny bit smaller.
European division REPRESENT!
DO WANT. Please, please, PLEASE don’t fill up before I get my fucking taxes back!
CAMP
CAMP CAMP
CAMP CAMP CAMP
CAMP^1000
Showoff.
Got it on the first try.
Wait..You’re both going? Fuck..I may need to go now
digger you have to come
DIGGER. WE MUST MEET. GET THE TO CAMP.
Digger! You have to come! To have a Golden Girls cabin reunion!
#lotsofexclamationmarksbecauseI’mexcited
#whiskey
Believe me, when Marika and Beez get together, explosions happen. Gay explosions. ^1000.
How do you know our secrets? Who are you, Herbal Tease? WHO ARE YOU.
Best case: I will once again be where the whiskey comes from…Worst case: $50 in the Autostraddle find! Registered Bitches!
OH MY GOD DIGGER YESSSSSSSSSS
Well..Riese said “Digger you have to come” And I always do whatever Riese says. So yeah..CAMP!
I’m GOING. I have registered! I just need money now.
Oh I was wondering, can there be a bisexuality workshop? I’d be really down with discussing my feelings of not-quite-fitting with either gay or straight society
I have a couple bisexual friends who are thinking of coming but are worried about how bi-friendly everything will be. A workshop like this would probably really help push them in the right direction. And you guys they ROCK! They should be there!
duh camp is everything-friendly! DIDN’T THEY READ THE RECAPS.
That’s what I told them! Camp is utopia!
I am a little tiny bit nervous about it tbh. Not that I think people will be mean, but I’m worried about feeling left out or not being represented.
I’m bi and I’m going, and I’m sure there will be others as well!
I found Camp to be pretty inclusive. That being said, anybody gives you any shit they will have to get through me to do it. And I don’t need the big scary gun to make my point. I got your back!
My gf and I are both bi, and we were both at the last camp and going to this camp, and it didn’t come up AT ALL. Nothing to be nervous about, everyone was completely accepting of everyone without even questioning how you identify.
Yeah, I would also be super into a bi/queer/etc. panel, I bet it would be awesome.
So close yet so far. Damn being a full time student.
ditto, yo. :(
Oh no, e! I am sad.
I AM SAD TOO. the good news is i graduate next may. The bad news is it’s next may.
Oh also I want to be in the naked cabin. Except I suspect the friends with me won’t want to see me naked, but I have no fucks to give. I’m just saying. Nudity/partial nudity cabin. I’m especially ok with it if it’s Annika’s.
Grrr I’ll be in school for this A-Camp :( crossing my fingers that the one in May will be after my finals next semester (but let’s be real, if it isn’t I’ll probs just go anyways because I’ll be kicking myself if I don’t)!
THIS. CAMP. so much yearning! I know you can’t tell us for sure due to the site’s schedule and so on, but how likely is it that May’s camp will be in the second half of May? I’m trying to decide between skipping the fourth week of exchange and flying over from the East Coast for September, or waiting for the next one to come before I fly all the way across the world again, and hoping it comes after exam week…
Singapore represent? :)
Fly from East Coast, of course! Sure beats flying 16-20h from this part of the world…..
I’m trying to decide between signing up for this one and just missing a few regular classes or waiting for the one in may and hoping it doesn’t conflict with my finals, gahh I think I’m leaning towards going to the September one, but idk!
Once again I like to point out that that is a picture of me dressed as mini mouse with ANOTHER picture of myself framed in the background.
That’s just how I roll.
CAMP
i always think that stef’s picture os her as mickey mouse but then i remember she’s wearing sunglasses, not ears.
I am so excited I registered on my phone while yelling to everyone around me about how awesome gay camp is.
Please please please do all the recaps of camp again- even though I didn’t go (and can’t go to this one, since I would be 10 to 6 days away from 18), it’s really awesome to read about how amazing autostraddle is in 3D. Maybe you could make the third camp in late May rather than earlier? Just so that college kids can go after exams. Good luck with everything, I’m sure it will be even more fabulous!
Yes or even JUNE for the next one. Stupid school is stupid for getting in the way of A camp, but would be over for most college kids by then.
My college didn’t finish until mid-June… and I’m sure the summer camps are in full swing then and it’s hard to find space for these things. Just saying. :/
Oh DAMNIT THAT IS PERFECTLY REASONABLE UGH.
I definitly just danced around at my desk. I CANT WAIT.
IS IT SEPTEMBER?!
There is already terrible talent show skit planning IN THE WORKS.
See you soon my precious pals!
Yess!!!
REGISTERED. I’ve been refreshing like a can of 7-UP all day.
OH GIRL
I won’t be at A-Camp, but if I were, here’s a workshop I’d like: “Teach me how to be a girlie-girl”. I mean, I’ve never learnt how to apply make-up, use product to style my hair, do an updo, stuff like that… I’m *clueless*!! And I’d like to learn. I can’t be the only one!
What do you guys think?
I like this idea! Last time soccer mom did a brilliant demo on applying eye makeup in the Troubletones cabin.
She really did! I was seriously just about to say this. :)
It’s also how I learned that magical things can happen when you just point and say “Do stuff to her face!”
i see lizz and sara medd being super into this idea
I feeling really in to this idea.
This is a fun idea! I’m definitely a makeup/hair product junkie. I don’t think I’m qualified enough to chat with a whole group, but I could teach people on a one-to-one basis :)
Oh! I’d also help campers get ready for the dance or talent show if needed!!
I would attend this workshop so much. I feel like an updo is something I should’ve learned before I hit my twenties. Teach me/us your pretty-haired ways?
Yes yes please please. I cannot for the life of me apply eyeliner on my lower lid. “Water line”? WTF.
WHAT. I have so many problems with upper lid eyeliner!!! There are so many things we can teach each other!
Don’t get me started on the lower waterline. I call it the “raccoon line” because that’s what I turn into when my unsteady hands smudge the crap out of it.
a lot of it depends on getting the right kind of eyeliner
I would totally attend this workshop.
YOU GUYS I LOVE THAT MY IDEA IS SO POPULAR. I FEEL SO VALIDATED RIGHT NOW! FEELINGS.
Registered! Checked the site between each class waiting for it!
Oh god oh god, May? That scares me so much, April is perfect, and May might be during midterms and then I might dieeeee.
Yes, I’m panicking about something that’s a year away.
lol I kinda am too, but Disco you have to come!
Yes, you must, because I will probably be able to make May, and then our bunny avatars could finally embrace, AS THEY ARE CLEARLY LONGING TO DO.
don’t tease me, tswizz
irl #showerbeer?
YES! registered! Now all I have to do is either spring for a plane ticket or resign myself to the 8 hour drive :)
i did the 8 hour drive and it was not completely terrible?
Any chance you’re from the Bay Area M? I’m checking out Amtrak and from my hometown to LA Union Station it’s only 65$ round trip. And someone else is driving, obviously, giving you plenty of time to read or surreptitiously play drinking games with Nalgene bottle whiskey.
Okay okay I may have lied- looks like $65 dollars back. So $130 round trip. Still, not shabby.
Yeah, I’m in the bay… Thanks for this, I may very well use Amtrak as I think my ability to drive will be impaired by excitement.
…That came out wrong. I’m from the bay area, not IN the bay.
From what I can tell, it’s anywhere between $60-90 less than flying out of San Francisco, Oakland, or Sonoma County. If you end up doing Amtrak and getting the Martinez-Bakersfield train as the main leg of your trip, we will most likely be on the same train and I’d love some company.
I JUST WANT YOU TO BE PREPARED:
http://www.autostraddle.com/transportation-review-amtrak-coast-starlight-823578/
also though i think it would be a kickass thing to do with a group of people, you guys should totally do it
That makes an airplane look really nice… Thanks for the warning.
Thanks for the heads up Riese! I took Amtrak from Martinez to Salt Lake City with my mom once and it was chill but granted we did spring for one of those train bedrooms. Also, the food was terrible and it was probably way more expensive than air travel. We just wanted to feel like old-timey, dapper broads. M., there’s a discussion going on with some other people from the Bay Area about getting together for Amtrak or carpooling on the next page.
The only Martinez-Bakersfield line that would go to Union Station would arrive @ 4:10 pm or later as far as I can tell… which is too late to catch the shuttle up to camp. However there is a train that goes from Stockton to Bakersfield that would arrive @ Union Station @ 2:30 pm. And if we end up on the same train, we should hang out.
I was also looking at the Martinez-Bakersfield train and was bummed to learn it would be too late for the shuttle and it doesn’t look like it will be possible to get to the Stockton-Bakersfield train from the Santa Rosa area in time either. :(
Santa Rosa represent! :D Even if the train idea just doesn’t work out, I think a Bay Area carpool would be awesome.
I want to ride Amtrak from the Bay Area to A-Camp (mostly because Taylor’s Amtrak liveblog made me feel like there where extra adventures to be had via train instead of plane.)
I just need to check with my work situation tomorrow, if all is well, I’m A-camp bound!
Bay Area peep over here, anyone want to carpool? :D I mean, I paid $120 for my round trip flight to get to A-camp and I fucking hate Amtrak so much after dealing with a long distance relationship.
Also I have never been to camp (because UK/Ireland) and the whole summer I was a counsellor in the US I was thinking “fuck fuck fuck I am SO SAD I never got to do this” because I knew I would love it and now I get to do it and with queer girls and weirdos and Autostraddle! And I am the happiest happiest happiest happiest and I cannot fucking wait. That is all. :D :D :D :D :D
THIS IS EXACTLY ALL OF MY FEELINGS. I DUN REGISTERED LIKE A BAWSSS
THIS! I’m from the UK and did the camp counsellor thing for a few years and was always so envious of the experience the kids got to have! Then I went to April A-Camp and it was like my wildest, most rainbow-filled dreams came true.
IS IT SEPTEMBER YET?!
Have fun everyone who can go! *weeps gently*
*weeps not very gently*
but seriously everyone, have an amazing time!
Just registered…excited out of my mind!
It’s 4 am in Tokyo, legit just stayed up all night refreshing waiting for this to pop up. Super excited, have no idea how I can justify skipping half a week of class the second week of the semester, but OH WELL REGISTERED AND GOING ANYWAY.
You have to justify this as a student, I may have to justify this as a teacher. Solidarity.
Indeed, now you just have to work on your phrasing and sell that shit.
“I’m going to cam-I mean, a conference. A women’s leadership conference…female empowerment, HOO-RAH!”
Exactly – Hopefully my cultural studies professor (whose research interests include: “Feminist and queer media and cultural production; transnational feminist and queer arts and activism;”) will approve. Shoot, if I have to write a paper on A Camp to justify it, I will!
If you have to write a paper AT A-Camp, we’ll make it a workshop titled “All of the Lesbians Write Alex!’s Paper Now”
I was going to go the standard “funeral for a fake great-great-great-aunt’s-cousin-thrice-removed-on-my-sister’s-side” route, or come down with a terrible bout of the Swahili Death Flu…but maybe a “conference” would go over better.
you never know, this could happen to you:
http://autostraddle.tumblr.com/post/23149238273/one-of-my-students-skipped-my-friday-lecture-to-go-to-a
I’d be simultaneously gratified & terrified if my little high-school freshmen saw pictures of me from A-Camp.
Let’s make this happen.
Me too, and it’s 2 weeks after school starts for the year…
People can get ill at any time, Emma. :innocent blink:
I have registered! Sober cabin here I come!
me too! me too!
I’m crawling out of the woodwork to say how insanely excited I am (and, also, you guys are amazing! Thanks for existing!)
#AutolurkerNoLonger
I feel like my actions of spending money on A-Camp again have been justified because I’m in one of the photo collages above! It was definitely meant to be.
hot damn, camp is already almost half-full
Last night I predicted that camp would be full by Wednesday. I’m going to change that to within 24 hours of registration opening up this morning. Amazing amazing amazing what you guys have created.
Hold. The fuck. Up. I need to check money, electricity and water just came out of my account and it caned me good, need to know if friend is on board, flights from London, potential job situation, I AM SO UNPREPARED FOR THIS.
good thing there’s another one IN MAY! (if you can’t make September)
A Camp starts on my birthday. That would be such a kick ass way to spend it. *fingers crossed that I can swing this*
My birthday is a few days after camp ends! party at A-Camp
Mine too! September 18th. I’m turning 22.
September 12! I love buying myself expensive b-day presents… Go Camp!!
Also, did Alex design the logo again?? It’s so wonderful. Pretty soon my wardrobe is going to consist entirely of Vega-designed Autostraddle shirts and I’m completely okay with this.
Yup, isn’t she so talented?
Design workshop with A;ex!!!
CAMP. I AM GOING TO A CAMP.
Aside, is it possible to register on behalf of someone else? Camp is a thing I would like to surprise my girlfriend with.
yes’m
um your girlfriend is really lucky!
i hope she agrees! she doesn’t know what autostraddle is, but she’s totally gay and loves camping, so.
I can’t imagine what camp is going to be like with twice as many people! So excited! SO EXCITED!
This was supposed to be a general comment, not a reply, but the internet hates me today!
The internet may hate you, but we sure don’t! :)
Happy for everyone who can go but also so so jealous. CAMP! <3
This is happening right after I get back from Chicago and start school! Well I’ll be going to Mills so hopefully it’ll be like A-Camp all year-round, except with papers and stuff. Have fun everyone! I will join you a few years down the line :-).
Registered!! Frantically called my dad so that I could use his paypal account. My explanation? “It’s this lesbian camp that will be the most amazing thing in the world…” Thank god for liberal parents.
OMGOMGOMG. I’ve been reading this site for so long and i’ve barely ever commented (although I did win a comment award one time, raise the roof) But now I am coming out of the auto-closet for CAMP! Fucking Camp!!!!!! ahhhhhhh!!! i can’t wait. at all.
I feel like A-Camp is what those 10 years of Girl Scouts were unknowingly preparing me for.
Oh my honor, I will try
To serve Autostraddle and company
To help my fellow queerz at all times
And to live by anti-oppressive-that-is-conscious-of-intersectionality laws
So, I am supposed to be packing to go be a counselor at Theatre Camp all summer, but I’m too excited about A FUCKING CAMP to concentrate!
Which theatre camp?
It’s in Phoenix :)
Ahh. Mine was NY but the starting date was around now so thought I’d ask :)
I am registered and this time I will keep my shirt on the whole time. Promise guyz :)
It’s ok babygirl, you do you. Especially if that means toplessness.
um I mean just be yourself
If you weren’t so generally adorable, that probs would’ve been creepy.
aww, that’s so weirdly sweet.
Assuming there are a bunch of Katie/Kate/Katherine’s again, we need to take a group picture! Same goes for all the Emily’s.
I am a Katie and I’ll be there!
there are 6 katie/kate/katherines so far!
Wow, that’s awesome! A group picture will definitely need to happen.
Ahh! I need to go! Waiting for roommate to call me back so i can use her debit card to register.. this is like the only thing having a bank account would be worth it for!
this is perhaps the best photograph i’ve seen from the morning-pirate-taylor-with-PBR series
morning-pirate-taylor-with-PBR.tumblr.com
I totally copied and pasted this thinking it was going to be a real thing, then I got sad :(
i don’t doubt that some enterprising A-Camper will make it so
challenge accepted
morning-pirate-taylor-with-PBR.tumblr.com
that is gaymazing
Just kidding! *dusts off credit card* A-Camp here I come!
Registered!!! Can it be September now?
OMG. dies. Whyyyy West Coast?!?! *sobs into pillow* I’m keeping my eye out for that scholarship because as a struggling recent grad, I might be able to scrape for tuition but not for the flight too. East Coast cats, we have mountains and nature-like things over here! It won’t be the same w/o the actual AS crew (maybe you guys can send over one or two representatives?) but I’m sure we can gather, organize and meet each other! I’m NY/NJ based! *sigh* It’s like Xena-Con all over again…yes, I just geeked out.
a few notes:
1) thank you to everybody involved in organizing this! i’ve done my fair share of organizing events/conferences/gatherings, but nothing this huge and exciting. you guys rule. i know how stressful organizing can be, so please be sure to take care of yourselves extra hard during these upcoming months. also, thank you for this again!
2) the majority of my work day, i feel, was refreshing autostraddle on my phone to see if registration was up yet.
3) i love everything about this.
I AM GOING TO CAMP!
Don’t you know baby yeah yeah I’ll be there
I’ll be there I’ll be there
Just call my name, I’ll be there (I’ll be there)
Just look over your shoulders honey! Oh!
I am really excited that I’ll know where you are for once.
Now we just need to get Waldo there and we’ll be all set.
http://yfrog.com/h77roprj
I might, I might explode from jealousy if DeAnne Smith attends this camp.
Come find me at camp!
dude now I’m picturing a Where in the World is Carmen SanDiego activity at camp, like hide and go seek or sardines, only gayer.
I will come to camp for this.
Can we call our cabin “Vagina Warriors” this time as an salute to Beth? Oh yeah..And THIS IS AWESOME!
What if…we turn 18 September 14th and we want to come really really bad? :(
Just registered and already I’m wishing it were september. I live in the LA area and am planning on driving up so if there’s anyone who wants a ride, just let me know!
Can I keep registering and backing out at the last minute? Can one trip really bankrupt me? As a grad student aren’t I already bankrupt? Will my life be the same if I never get to discuss J Crew and Anthropologie with Lizz? Maybe I can’t afford the trip because I buy too many clothes. Someone should tell me what to do.
well you should definitely go.
I’m registered and i’m recruiting! One said “I think I will do it, but that price tag is a little steep! Well worth it?” OF COURSE
I’m always recruiting!
Do you get lots of toaster ovens?
When lesbians are involved, there are ALWAYS *appliances*
So I just registered. It makes me want to throw up, but in the best way possible!!
It will be awesome. You will be awesome. And if necessary, I will hold your hair back for you.
I’m hoping to have the anxiety induced vomiting under control by September. But if not, I’m looking at you, Digger.
I just registered and Paypal asked if I wanted to pay later…it’s like even the internets know I’m broke!
Registered!! Oh em gee. This day just got one million times better
I so completely want to do this, and it’s SO CLOSE to being workable, given that I’m about to graduate college and am coming home to CA this summer/fall/????. But I can’t make any plans for later than mid-August until I know about my job situation for the fall.
ENDLESS SADFACE.
this is why you’re infinitely more responsible than i am. i don’t know my job situation for 2 weeks from now, and i’m still going. i’ll find a way to make it work!
I was too excited and I didn’t see the address to send my registration check… Anyone?
When I registered it said to e-mail [email protected] for check payment info.
Merci!!
(crafts + hiking + cabins > whatever the fuck goes on at the dinah) x infinity #math
what, wait, what? are you coming?
DON’T EVEN!!!!
*tries to calm down*
IS HEATHER HOGAN. COMING TO A CAMP.
WELL IS SHE?
I’ll be in a cabin in Wisconsin with my girlfriend and probably ten grizzly bears when this thing goes down, so I’ll just have to live vicariously through you guys!
that’s so disappointing, I was hoping we could bond over our excessive love for Naomily, who lives forever in my heart.
Gutted. Heather you’re one of the people I owe a gratefulhug, I thought I was going to get to cross another off the list that weekend.
Oh well. Someday!
you can hug me an extra time for heather, and then i will text her and let her know how it felt
Riese this is a deal.
Actually, I owe Riese several grateful hugs — her L Word recaps are one of the things that helped me learn to write — so you’ll be doing me a solid passing that on to her. (Is getting threesomes started always this awkward?)
I’m actually very good at getting threesomes started so we’re gonna be just fine.
Holy cannolis, this is so EXCITING! I’m already thinking about what goes into the train survival kit for the 34 hour ride from Seattle. OMG CAMP
so so jealous of everyone who comes by train!
I thought about taking a train from NY, but it turns out that would be a 64 hours train ride, and cost about as much as flying. No thanks!
*Generic comment about not being able to come this time*
*Generic comment about the fact I just made an innuendo*
I wish all you lovely lady-loving ladies the time of your life in September and will be very jealous of your outdoorsy fun times.
I’m pretty sure a large chunk of my excitement about this stems from all the boarding school books I read as a kid. And I’m going to come by train. Oh my goodness, girls in books always went by train and the wheels made happy sounds.
sometimes i feel like i maybe invented camp because i wanted life to be like boarding school again
Reason enough.
I want to go to there.
Autostraddle Camp is now my # 1 life goal. It comes before university or my dreams of owning a kitten farm with Ellen Page. IT WILL BE A THING FOR ME
KITTEN FARM.
I HAVE TO MAKE THIS HAPPEN.
Can I be one of the gay cowgirls at your kitten farm?
I just signed up for this and I am super stoked and super anxious at the same time. I have never been to camp, any camp at all! And I’m a few months into my transition. And I think I’m using my Outside Lands money for this instead which is probably worth it. But damnit I’m taking this opportunity and I can’t wait to share in all the rainbow goodness with y’all!
SO EXCITED YOU GUYS
All I want to do is watch Bug Juice.
if i could + this x a million, i totally would. also yesterday i found a VHS of bug juice that i recorded from the tv. i may have to start watching it.
i hope my a-camp cabin counselors are luna and annie!
I’m now watching Bug Juice on Youtube and looking up all of the counselors and campers on Facebook. Already found Rhett.
OMG
Oh man, I’m normally not someone who would do this sort of thing, but I was TOTALLY SOLD with the recaps.
And hey
you know the motto.
YOLO.
carly’s pic is the best pic
My heart. It breaks.
But not spending the past 3 years of my life in vain trying to complete school just to skip the final portfolio review and not graduate is pretty cool too. I guess.
>.<
Because I have finals when most people are starting the second week of school…? Year round art school is a weird thing, guys.
I wish I was in America.
I had signed a contract to start a job in September, but A-camp runs into two of the mandatory training dates. So I resigned. And then registered for this.
Priorities.
:-)
I would like to take some credit for this excellent decision!
Your welcome Jacq for introducing you to the glory that is autostraddle. WE’RE GOING TO CALI!
Credit granted! Who needs the first week of school, or money, or a job anyway?
A-camp ahoy. :D
I like you Canadians already. :D
wow this is so reckless and awesome! You go! The universe will pay you back for your good priorities with a new and even more awesome job, I’m sure.
I’m trying not to think about it too much, but that’s totally what I’m hoping for haha. Everything’s supposed to happen for a reason, right?
Sigh..To Camp..Or not to Camp
That is the question… and you know the answer: CAMP!
Silly question, Digger. I say again…GET THEE TO CAMP.
CAMP CAMP CAMP CAMP CAMP
Last time I said, “I’ll be at the next one!” but I think I’m going to have to say “next time” again. Damn…
Registered! And I think I shall take the beginning part of the week off as well to mosey on down to the San Diego beaches.
I’M SO JEALOUS WHY CAN’T I GRADUATE 2 WEEKS SOONER
D: D: D: D: D: D: D: D: D: D: D: D:
Yes, sometimes being an adult and not having to deal with that school business works out. Plus, school….boooooo
Well… … … I’ll be an adult and not have to deal with school soon.
2 weeks after a-camp, actually.
._.
A-camp 3.0 will be my time.
I AM SO EXCITED TO TOUCH ALL OF THESE NEW FACES
now i just need to get started on memorizing your names
update – 68% full
If you manage to memorize twice as many campers as last time, you will be my eternal hero.
Well, you already are, but…even more.
I told my mom that i’m going to camp. This is our convo after I explained what camp is.
“thats great krysta, i am so happy for you”
“thanks! my first time at camp!”
“your first time? i- oh yeah i wouldnt count those years at (mormon) girls camp either. im sorry i made you go to those. It must have been awful”
“so oppressive”
“you did get to go white water rafting”
“oppressive rafting mother!”
your mom rules.
I keep rereading “oppressive rafting mother!” and I love it more each time.
*sigh*
A-Camp 2 will be happening during the second week of my first year of law school. As much as I would LOVE to skip class and fly to California, my responsible brain won’t allow it. I already miss the days of undergrad slackerdom.
Maybe I’ll be able to make the A-Camp in May (but for the love of Rachel Maddow, please make it late enough in the month so that final exams will be over.)
I’m currently working this Victoria Day holiday (boo-urns!). The fact I’m still paying off recent vacation expenses, the additional time and costs flying in from eastern Canada, the dates are during an almost non-negotiable blackout for work and the interesting time explaining that I’ll be with a bunch of other amazing unicorns to my old-school-conservative, borderline racist/homophobic Catholic mother I have yet to come out to were hardly deterrents/irrelevant the moment I saw open registration for Fall A-Camp. I went into tunnel vision and surrendered my PayPal account on the spot (which turned my “Boo-urns!” into a “Woo-hoo!”).
CAMP. WORTH EVERY PENNY.
love this
So…I’m not quite 18. Like I’ll be 3 months away from 18 in september. someone tell me it might be possible to still go to A-Camp? i REALLY REALLY REALLY WANT TO GO HANG WITH QUEER LADIES.
Come in May!
please excuse my millionth comment of the day, but. guys i just remembered something. frequent flier miles! they will get me to camp for a very reasonable cost!
how fetch would it be to write/see a piece on economically creative ways to travel to a-camp? the possibilities are endless!!! (frequent flier miles, freighter ships, train hopping…)
You just made “fetch” happen.
The problem is all inside your head
She said to me
The answer is easy if you
Take it logically
I’d like to help you in your struggle
To be free
There must be fifty ways
To get to A-Camp
She said it’s really not my habit
To intrude
Furthermore, I hope my meaning
Won’t be lost or misconstrued
But I’ll repeat myself
At the risk of being crude
There must be fifty ways
To get to A-Camp
Fifty ways to get to A-Camp
#paulsimon
SIGH. Maybe *next* next time then… or the time after that.
ONE DAY!!
*Goes to YouTube Bug Juice clips*
basically i’m upending my life, quitting teaching, moving out of state, applying to grad school, and have no clue what i’m doing after june 15. except for the fact that apparently i just registered for CAMP WTF.
excited for the ensuing convo with my mother- she’s going to be more excited than i am!!
I’m so bummed I can’t come this time around. It’s basically my first week of college (which is equally as exciting as A-Camp, but I can’t miss it.
Laneia- I’ll teach the sewing circle at A-Camp 3.0 :)
i was just thinking about you last night! totally sad you won’t be there, but will look forward to A.3
may have just registered for A-camp even though I’m not 18 and i didn’t check with my parents….. WHATEVER. rebel.
may have really enjoyed this comment.
I like you already
Graduation = free Septembers. This may be the thing that makes me happiest about graduation.
I’m excited to meet a lot of new people and to make a lot of lifelong memories and inside jokes. I’m coming to camp by myself. I’m sure the people in my life probably think I’m going to be killed by some serial killer in the woods.
I’m more than willing to take my chances.
Omg. Serial killers live in the woods. THIS IS REAL. I’m also willing to take my chances though.
We need East Coast A-Camp because I am too broke to trek out to California but I still want to make up for t own awful girl guide camp memories.
Registered, y’all! And I am making the trek from Massachusetts so you know I mean it when I say I am SO. DAMN. EXCITED.
Any other A-Campers coming from this neck of the woods?
Yes, there’s quite a few of us flying out of Boston! There was talk about us all flying together.
Flying out of Boston here too! I’m sure there’ll be a ton of us what with all the schools there. It’d be hilarious if we all boarded the same flight at Logan
I’ll be in California before camp starts, but flying out of LAX on Sunday afternoon (2:45ish) back to Boston. Has anybody else booked flights yet?
NOOOO! The ONE weekend ALL AUTUMN that I already have committed plans? NOT FAIR (really, is one’s sister’s wedding really more important than lesbian camp? She’d understand, right? …)
oh my GOsdkSH I’M REGISTERED! bringing the party all the way from south louisiana.
Seems crazy to have just registered to go off to the woods with a big group of people I don’t even know, and yet I am SO EXCITED!
I know exactly what you mean. I am doing the same thing! Here’s to making friend with strangers :)
I’d rather live saying “oh well” than “what if”!! :D
will there be bay-area-ers driving down/ do people want to carpool from the bay area so I don’t have to drive down alone and pay for gas!!!!!!??
I will most likely be Amtraking it up from the bay area! Join me!
oh that sounds like an excellent idea! its not very expensive and involves no driving or airplanes!! let’s keep in touch about that, we can totally treck (is that a real word? maybe?) it on amtrak together!
I’m from the Bay Area too! And still not quite sure what transportation I’ll be taking…
I’ll most likely be coming down from the bay area then too, I’m totally down to coordinate something
Riese posted this warning about Amtrak: http://www.autostraddle.com/transportation-review-amtrak-coast-starlight-823578/
However, I think it might be fun if we can get a group together to hang out on the train and make the most out of the crappiness that often is train travel and bask in our collective excitement and queerness. Or if train travel gets voted out, I’d be equally down to arrange a carpool.
I think that going by train still sounds sounds amazing as long as we can get a decent group together. Road trips are fun too.
Based on Riese’s article I think I’d rather drive with lots of people. We could rent like mini-van if there are lots of us? Or use somebody’s car and all chip in for gas and then we can make new friends yayyyyy
I am not a fan of this particular train, but it does sound much better with a group of A-campers…
yeah it’d be better in a group — but don’t count on it arriving on-time, is the thing. Taylor trained down from portland and had a great time, but she was coming in two days early for pre-camp festivities, so timeliness wasn’t so much of an issue for her. but i think it would def be more fun if you had a group of friends.
i don’t have a car, so every time i go to LA, i have to rent a car, and it’s not that expensive really — it’s actually cheaper to rent it for an entire week than to rent it for 5 or 6 days, oddly. I think my last rental car was like $200 for the week, but it was tiny. as long as the renter is over 25. just get some mini-vans and caravan! then also you can stop and get booze on your way, if you so desire. if you split the cost between everybody it’ll also be cheaper than the train.
I have a car that seats 5 people (including me). So if 4 others want to drive down w/ me in my 11 year old Audi I’d be down. And we could split gas 5 ways which would be cheaper than amtrak. and then we could stop for food and stuff.
That could work.. We could also take my car if more people wanted to come.
ALSO — if you take amtrak, you’ll need shuttles from the airport to camp, which’ll cost more $$ for each of you. if you drive, you can drive all the way to camp and not need shuttles!
My truck only seats 3 including the driver and is a ragged beast, but I am definitely down to chip in gas money and booze money and bring snacks for whoever is driving.
My car is a ’08 toyota camry hybrid that seats 5 BUT idk if it could hold that much luggage… BUT! I might be able to get a hold of this ancient suburban that holds I think 7… OR I could probably borrow my dad’s truck which seats 5 but would hold all the luggage anyone wants.
Well it sounds like we have at least 2 potential cars for our Bay Area group… Awesome!
Woo! Should we get each others emails so we can better organize this?
What part of the bay do you live in? I’m wondering how we’re all going to meet up. I could probably get a ride into the city if we decide to meet there.
I’m in Marin and could probably pick up North Bay people and bring them to whatever the meeting spot is…
Carpooling sounds great to me!
How would you bay area folks feel about pit-stopping in SLO? I’ll pitch in for all the things, of course :)
That’d be fine with me. I think the bigger group, the more fun it’ll be.
Me & my gf are registered and totally looking to carpool from the Bay. Keep us in mind, plz? :D
By the way, I can pick people up in Marin or in San Francisco. Any east bay folks out there?
I’ll be coming from Berkeley! But for real, let’s do some carpooling. Don’t think I’ll be able to drive yet but it’s a possibility.
I say we figure out a way to start some sort of area-carpool-sorting post?
YAYAYAY!
facebook group.
no not a facebook group. i have no facebook!! or if there is one will someone keep me in the loop?
Ok, doesn’t have to be a facebook group! All good. We’ll figure something out. Yay for Bay people!
True life: One of my out of town friends once took an Amtrak train to come visit me, and in the time it took for her train to arrive I could have driven to her house, picked her up, stopped for a picnic, driven back to my house, and it would have been about 1/3 the cost.
well, if the european division decides to represent for real we might start our visit to the us in the bay area….
I am driving to camp from Oakland, as long as my car is still running……Maybe there will be a fall a-camp group where we can coordinate closer to September?
I’m in Oakland and totes down to carpool with people if that’s a thing that’s happening!
I guess I would need to know for sure before the point where the price of plane tickets starts to go up so I don’t get stuck paying a million dollars.
So this is during classes and I really can’t skip them + Boston airfare puts it a little out of my college budget, but May’s camp may or may not be influencing my decision to look for co-ops in the Cali/LA area for next spring/summer.
concerns my mother had when I told her about this and lied saying it would be substance free- if i would be having sex.
I just told my mom that it was a young women’s empowerment camp…..
I have no fucking clue whether I will be living in FL or WA in September, I have no fucking clue how I’ll be able to afford $365+ transport, BUT I AM REGISTERED AND I DONT CARE BECAUSE I AM TOO EXCITED and I’m sure I’ll figure it out. Hopefully I’ll already be settled in Seattle and it will all be significantly easier than if I am still living in Florida and trying to move out West…
Have to be over 18? Damn it. Well, I guess this would be incredibly awkward to explain to the family, so it’s not like I’d be able to go anyways. I hope A-Camp will still a thing that happens in a couple of years when I’ll be on my own and able to get away with excuses, as opposed to having to explain everything in detail to everyone. Time to start thinking of creative excuses. I don’t think I can top “Lesbian Christian Feminist Camp,” though.
under 18 and registered for camp. be a rebel with me!
I kinda feel like Autostraddle would really love it if you were over 18 because liability issues? Pretty sure it’s not personal.
Can’t focus on studying for my finals….because I’m still SO excited about registering (even after 12 hours have passed). I don’t know how to handle this excitement….
YES. My birthday happens in here! YES.
Totally registered in a snap decision moment. Then realized how many days we were talking about here. I just started working at a school. I don’t know if I’ll be eligible for days off yet. The probation period lasts, like 6 months. Fuuuu. I will figure this shit out. I missed the first A-camp because I hesitated too long. I am not going to miss this one. I hope.
Never been so sad that I live in the UK. This is disneyland all over again.
I can’t make it to this one (two trips to the other side of the world in one year is a bit too much for my bank balance!). But i’m planning on coming to the next camp – May next year should work for me :)
Anyway, hope all of you going along to A-Camp 2 have a wonderful time!!
Riese, I am so so happy that May’s A-Camp went so fantastically – not for the team, who seem to have had the most exciting and fun-filled weekend of their lives, not for the regular Autostraddlers who finally found a community where they felt normal and comfortable and loved, but for you. The brave, special person who, instead of hoping to just stumble across somewhere that felt like home for people like us, actually worked (and still works) a mind-boggling number of hours to make that happen. You have all of my love and respect and admiration. You’ve truly, genuinely changed my life, and the lives of thousands of others, and I’ll always be grateful for that.
Your dream has become a reality! Congratulations!
(Sorry for the length and sappiness of this, but I really just had to say it.)
aw, thank you!!
Oh I want to go to A-Camp SO MUCH after reading the recaps!
Damn unemployment! So tempted to raid my savings and just hope I get a job in the next few months to pay for it.
This is amazing! You all are amazing!
Can’t do it this year but after that… watch out everyone XD
I’m going.
I’m going. I’m GOING!
AW YEAH YOU ARE
Fairy gaymothers are real, y’all.
I was just forced to register by some random Sexo. See you there queermos.
brandy has a way with women…
Truest of all the true stories ever told.
I want to go so bad!
I have also spent about $6000 on vet bills in the past few months, with much more to come, so I guess I shouldn’t. Dammit.
DONE!!!! I am so so excited!! I don’t know how I’m going to handle the wait now….
I’m going to freaking A-camp!!
Is it normal to be going alone?
I come from a small homophobic town in riverside county; you can be out, but you’ll be alone.
I’m going with Team Lesbiate..which consists of only me, so. I went on my own for Dinah as well. So I mean – you’re going alone – but it’s not like a “forever alone” alone, y’know? Just surrounded by random queer lady people alone..which is good.
BASICALLY WHAT I’M TRYING TO SAY IS THAT YES IT’S TOTES NORMAL.
Yay! Thanks Cynthia!
I could not sleep until about 3am this morning I was so excited!!
Summer camp I’m actually going to enjoy!!
I’m going by myself too! I think we’ll be fine :)
in april about 66% of our campers came by themselves not knowing anybody. you’ll be ok!
I’m also going alone. We’ll all make friends!!! :D
I’m totally going alone as well no worries! :]
I’m going alone too!
OMG I’M GOING
So that’s cool.
Oh. I was so close to saying “fuck it let’s do it” and just registering and hoping I could find a job/sell enough of my worldly possessions to make up the amount before September, then I found out how expensive flights to the US are.
Damn world geography. Sadtimes.
Oh my gosh! I about had a heart attack when I realized this had been posted on Monday and I hadn’t registered yet and WHAT IF THERE WEREN’T ANY SPOTS LEFT. But everything will be okay, I’m all registered now.
…eeeeep!
How do I pay by check? No one has answered my emails :[
i registered. impulsively. because it’s gonna cost me a fortune but it’s one that will probably get me laid… i mean, will be an enriching life experience.
ALSO just checkin’ in — the blurb up there says “female-identified folks” but i assume the camp is open to people who identify otherwise…right?
Hey guys! For those that can’t afford a plane ticket and driving is to arduous or damn expensive cause it is…, don’t look over taking a Greyhound (bus…lol) to camp! It’s probably MUCH cheaper than driving yourself if you’re not carpooling and it’s nice and comfy! That’s how I’m going to get to A-Camp in May :D
Sigh…I am an undergraduate and have class in September. I also just spent an obscene amount of $ to make sure my girlfriend and I will be attending ACL (aka seeing Tegan and Sara) in October. I will start saving and planning for A-Camp 3 next May (and maybe bring my sister with me)! Can’t wait, although I really really reeeeally hope Hannah Hart will still be a part of these at that time cause that girl is hilarious/adorable.
I really want to come! Someone should invent this in Australia. Have fun all you lucky kids
I’ve been reading Autostraddle since it started, but I just became a member, AND I JUST REGISTERED FOR A-CAMP!!!!!~~~~~
I’M SO EXCITED, PEOPLE!!!
I can’t believe that I’m missing A Camp again because I’ll be a counselor at for a camp-like program! I much rather be at A Camp than working… :P
I feel like I’m missing out on life.
*frustration*
I HOPE EVERYONE HAS A GREAT TIME! :D
I’ve read everything available on A camp and I check my email like 100 times a day. It’s going to be quite the wait for this happy camper.
Welp, I have very little money and no job (yet?), and I’m not sure in which state I’ll be living come September, but I just registered for camp and I’m happier than I’ve been all year.
Is A-Camp open to non-female identified folks?
(I absolutely understand if its a female-identified only space, I was just wondering if folks that do not identify within the gender binary would be welcome)
If you reserve a spot and then decide not to go is it transferable?
So burning man ends a week before, so i’d be on that coast… all i would need is a way to occupy myself in the area for a week first… I think i could drag my post burn dusty self there.
Is anyone else going to burning man before?
(Also first Autostraddle comment yay!)
registered and so beyond excited !!!!!!!!!!!!!!!!!!
JUST BOUGHT MY PLANE TICKET.
i am so anxious for more a-camp 2012 posts.
a 26 hour road trip sounds pretty tantalizing as I sift through the previous A Camp recaps.
my bank account is telling me no, but my body, my body is telling me yes
I have never been this jealous of fortunate people. I am a pretty content person and I have always believed that jealousy is the ugliest trait. But then again sometimes it just hurts. Also, it makes me feel kinda sad that I am stuck here in the Philippines and that even Google Maps cannot calculate the miles on how far it is from here to the camp site. But on the bright side I am genuinely happy and super excited for those who will be able to attend and I wish nothing but the best for y’all. I am looking forward to a lot of pictures and stories about this. I am also daydreaming that a fairygaymother would fly me there sans the VISA. Or perhaps an overseas A-Camp that’s closer to me, haha, me to myself: “keep dreaming jay” ^____^
OMG. Flying to the United States of the Americas is not for free!!! I was super excited when I saw a flight price for 279$, I was like high fiving myself, finally my ninja flight searching has paid off then I realized it was 279$ each way which equals about a million dollars more than I thought it would cost!!
Yes! I’m in! My name came up! I registered, I bought a plane ticket, I can’t stop telling everyone with in five feet of me that I am going to lesbian summer camp!EEEEEEEEEEEEEEEEEEEEEEEEEEEEEEE!!!
okay, deep breath.
Oh, and I just got the email today about the pool being open.
I seriously can’t stop thinking about camp. Every night I have dreams about how much fun this is going to be.
OMG, what am I going to wear?!
I am so there next year!
I would be 18 literally like 2 weeks after camp. No exceptions? I would really love to be a part of this :)
*Ciarra~babydyke
I wish I knew about A Camp!!! I could cry right now! I’m in the states at the moment and was in California that whole time! Booooooo!
*visiting from Australia